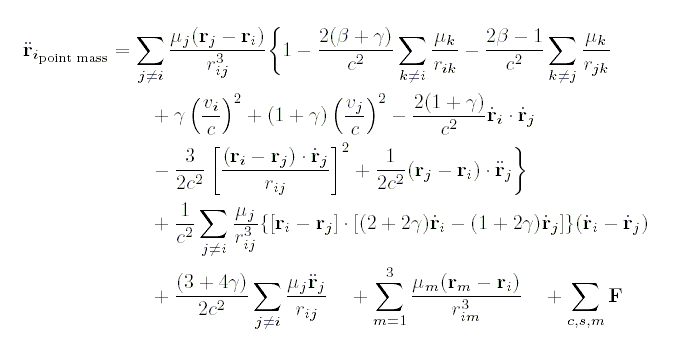
|
(1) |
Orbital Ephemerides of the Sun, Moon, and Planets
presented by E. Myles Standish and James G. Williams
| до того | Содержание | после того |
Орбитальные эфемериды Солнца, Луны и планет.
Е.Майлс Стэндиш, Джеймс Г.Вильямс
3. Уравнения движения
Уравнения движения описывают силы, действующие на планеты, Солнце и Луну и регулирующие их движение, и момент сил, приложенный к Луне и влияющий на ориентацию осей инерции Луны. Мы полагаем, что уравнения, представленные в этом разделе, корректно и в полной мере моделируют движение небесных тел на уровне точности наблюдательных данных. Другими словами, при заданной точности наблюдений нет повода предполагать наличие иных сил в Солнечной системе, чем те, что приняты во внимание. Неопределённости, существующие в движении Луны и планет, уверенно объясняются учётом погрешностей наблюдений и процедурой улучшения начальных условий и динамических постоянных.
Основные положения этого раздела разрабатывались в Лаборатории реактивного движения в течение нескольких последних десятилетий. Формулы, представленные здесь, включают также ссылки на их описания в прежних публикациях.
Уравнения движения, использованные при создании DE405/LE405 включают вклад от следующих факторов: (a) взаимодействие точечных масс между Луной, планетами и Солнцем; (b) общая теория относительности (параметризованный пост-ньютоновский подход при выборе "изотропных" координатных условий); (c) ньютоновские возмущения избранных астероидов; (d) действие на фигуру Земли со стороны Луны и Солнца; (e) действие на фигуру Луны со стороны Земли и Солнца; (f) физическая либрация Луны, моделируемой как твёрдое тело , обладающее приливными и вращательными искажениями и включающее как эластичные, так и диссипативные эффекты; (g) эффект на движение Луны, производимый приливом, возникающим на Земле под действием Луны и Солнца, и (h) возмущения от 300 астероидов в движении Марса, Земли и Луны.
3.1. Взаимодействие точечных масс
Основные гравитационные силы на девять планет, Солнце и Луну моделируются как взаимодействие точечных масс, соответствующих этим телам, на основе параметризованного пост-ньютоновского подхода (PPN) к проблеме n-тел для метрики, определяемой "изотропными" координатными условиями (Will, 1974). Уравнения движения n-тел были получены Эстабруком (Estabrook, 1971a) методом вариации независящего от времени интеграла действия Лагранжа и сформулированы в невращающейся прямоугольной системе отсчёта с началом в барицентре Солнечной системы. Включены также ньютоновские гравитационные возмущения от 300 астероидов, выбранных по причине оказываемого ими ощутимого эффекта на взаимное расстояние между Землёй и Марсом на интервале времени точных измерений дальности с помощью космических аппаратов.
Для каждого небесного тела i ускорение, обусловленное взаимодействием точечных масс, даётся уравнением
где
 - вектор положения, вектор скорости и вектор ускорения тела i ;
- вектор положения, вектор скорости и вектор ускорения тела i ;
 ,
,
 - гравитационная постоянная,
- гравитационная постоянная,
 - масса тела j ;
- масса тела j ;

 - PPN параметр, мера нелинейности гравитационного поля;
- PPN параметр, мера нелинейности гравитационного поля;
 - PPN параметр, мера кривизны пространства, порождаемой одиночной покоящейся массой (в нашем варианте интегрирования, как и в общей теории относительности,
- PPN параметр, мера кривизны пространства, порождаемой одиночной покоящейся массой (в нашем варианте интегрирования, как и в общей теории относительности,
 ) ;
) ;
 и
и
 - скорость света.
- скорость света.
Величина
 , появляющаяся в двух слагаемых правой части уравнений (1), означает барицентрическое ускорение каждого тела j, обусловленное ньютоновским притяжением остальных тел и астероидов. Таким образом, правая часть уравнений зависит от левой части, и, строго говоря, вычисления должны быть итерационными. Тем не менее, использование для этих членов ньютоновских ускорений обеспечивает достаточную точность.
, появляющаяся в двух слагаемых правой части уравнений (1), означает барицентрическое ускорение каждого тела j, обусловленное ньютоновским притяжением остальных тел и астероидов. Таким образом, правая часть уравнений зависит от левой части, и, строго говоря, вычисления должны быть итерационными. Тем не менее, использование для этих членов ньютоновских ускорений обеспечивает достаточную точность.
В предпоследнем слагаемом правой части (1) величины с индексом m относятся к трём большим по массе астероидам (“Big3”): Церере, Палладе и Весте. Последний член представляет силы, обусловленные действием 297 других астероидов только на Землю, Луну и Марс. Малые тела сгруппированы по трём таксономическим классам (C, S, M).
Силы притяжения от астероидов были вычислены следующим образом.
3.2. Барицентр Солнечной системы
В релятивистской постановке задачи n-тел все динамические величины выражены по отношению к центру масс системы, определение для которого отличается от обычной ньютоновской формулировки. Выражение для барицентра Солнечной системы было дано в работе (Estabrook, 1971b):
где
и  - гравитационная постоянная умноженная на массу тела с номером i,
а
- гравитационная постоянная умноженная на массу тела с номером i,
а  - барицентрическая
скорость тела с номером i.
- барицентрическая
скорость тела с номером i.
В реальном процессе численного интегрирования оценивались и интегрировались только уравнения движения Луны и планет. Барицентрические положение и скорость Солнца были получены на основе уравнения барицентра. Следует заметить, что поскольку каждое из двух уравнений барицентра зависит от другого, то для оценки положения и скорости Солнца требуются последовательные приближения.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |