В рамках современной модели движения планет Солнечной системы записаны уравнения движения далёкого спутника планеты-гиганта в прямоугольных планетоцентрических координатах.

Массу Солнца обозначим , массы планет обозначим для значений индекса .

Рассмотрим движение спутника планеты с номером и массой . Массу спутника обозначим .

Центр системы координат поместим в центр планеты с массой . За основную плоскость примем плоскость эклиптики, фиксированную на эпоху J2000. Ось направлена в точку весеннего равноденствия эпохи J2000.

Пусть в выбранной планетоцентрической системе отсчёта заданы
- вектор положения спутника, ,
- вектор положения Солнца, ,
- векторы положения планет,
где , но

Дифференциальные уравнения движения спутника в прямоугольных планетоцентрических координатах имеют вид

Рассмотрим влияние на движение спутника основного возмущающего фактора - Солнца.

С помощью возмущающей функции

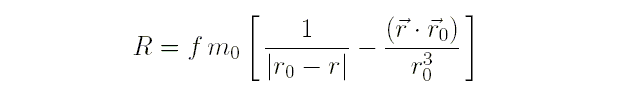
запишем дифференциальные уравнения в виде

Выполним разложение возмущающей функции с точностью до второй степени отношения расстояния от планеты до спутника к расстоянию от планеты до Солнца .

Вектор положения спутника относительно центра масс планеты имеет координаты

Пусть теперь вектор с координатами - вектор положения планеты относительно Солнца,

Приближённое выражение для возмущающей функции принимает вид

Использована формула для полинома Лежандра второго порядка

Вернуться на страничку
Движение далёких спутников