Перевод статьи
http://iau-comm4.jpl.nasa.gov/XSChap8.pdf .
Orbital Ephemerides of the Sun, Moon, and Planets
presented by E. Myles Standish and James G. Williams
Орбитальные эфемериды Солнца, Луны и планет.
Е.Майлс Стэндиш, Джеймс Г.Вильямс
10. Кеплеровские элементы орбит для приближённых вычислений положений больших планет
Формулы для вычисления положений планет, обладающие низкой точностью, имеют ряд важных приложений в тех случаях, когда не требуется высокая точность эфемерид. Их часто используют как при составлении расписания наблюдений, наведении телескопа и предсказании некоторых явлений, так и при планировании и проектировании космических миссий.
Приблизительные положения девяти больших планет могут быть найдены на основе формул кеплеровской орбиты и начальных числовых значений элементов орбиты и скоростей их изменения. Приводимые в таблицах параметры нельзя называть "средними значениями" в том смысле, как это принято в небесной механике.
Числовые значения элементов орбит и скоростей изменения элементов
получены
в результате сравнения с мгновенными значениями гелиоцентрических координат планет под одним условием: при использовании этих параметров в формулах кеплеровского движения среднее квадратическое отклонение должно
быть минимальным на заранее заданном промежутке времени. Как следствие, следует отметить, что наборы элементов становятся неверными за пределами интервала времени, на котором они получены.
(Разумеется, что параметры, приводимые в таблицах, не имеют никакого физического смысла и не могут служить причиной каких-либо теоретических выводов. Применение их ограничено списком практических задач, упомянутых в начале раздела.)
Повторим ещё раз, ибо это важно. Числовые значения элементов, приводимые в таблице 10.2 или в таблицах 10.3 и 10.4, зависят от интервала времени, на котором они получены и внутри которого их можно использовать.
В следующем подразделе даны формулы для использования этих элементов.
10.1. Формулы для использования кеплеровских элементов
Ниже в таблицах приводятся числовые значения следующих кеплеровских элементов:
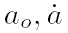
|
: большая полуось (астрономическая единица, астрономическая единица в столетие),
|
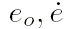
|
: эксцентриситет,
|
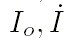
|
: угол наклонения (градусы, градусы за столетие),
|
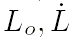
|
: средняя долгота (градусы, градусы за столетие),
|
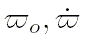
|
: долгота перигелия (градусы, градусы за столетие),
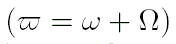 , ,
|
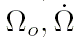
|
: долгота восходящего узла (градусы, градусы за столетие),
|
Для того, чтобы определить координаты одной из планет на заданную юлианскую эфемеридную дату 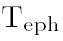 , надо выполнить следующие действия:
, надо выполнить следующие действия:
- Вычислить значение каждого из шести элементов этой планеты, например,
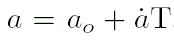 ,
,
где 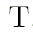 - момент времени в юлианских столетиях от эпохи J2000:
- момент времени в юлианских столетиях от эпохи J2000:
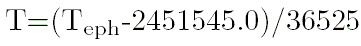 .
.
- Вычислить значение аргумента перигелия
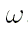 и значение средней аномалии
и значение средней аномалии 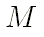 :
:
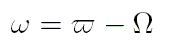 , ,
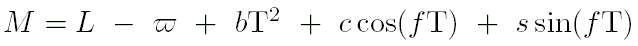 , ,
|
(30)
|
где три последних слагаемых следует добавить к значению элемента 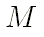 для внешних планет от Юпитера до Плутона при использовании формул на интервале времени от -3000 до +3000 лет.
для внешних планет от Юпитера до Плутона при использовании формул на интервале времени от -3000 до +3000 лет.
- Привести значение средней аномалии к промежутку
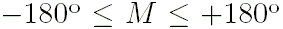
и затем получить числовое значение эксцентрической аномалии 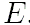 путём решения уравнения Кеплера:
путём решения уравнения Кеплера:
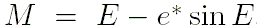 , ,
|
(31)
|
где 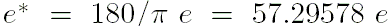 .
.
- Вычислить вектор гелиоцентрических координат планеты
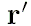 , расположенный в её орбитальной плоскости, с осью
, расположенный в её орбитальной плоскости, с осью 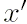 , направленной из фокуса эллипса в точку перигелия:
, направленной из фокуса эллипса в точку перигелия:
- Вычислить вектор
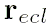 , лежащий в плоскости эклиптики, фиксированной на стандартную эпоху J2000, с осью абсцисс, направленной в точку равноденствия:
, лежащий в плоскости эклиптики, фиксированной на стандартную эпоху J2000, с осью абсцисс, направленной в точку равноденствия:
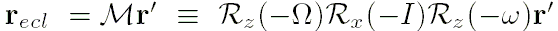 , ,
|
(33)
|
или, в координатном виде,
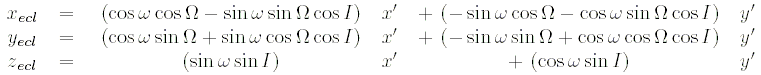 , ,
|
(34)
|
- При желании можно получить компоненты вектора положения объекта в системе фиксированного экватора "ICRF":
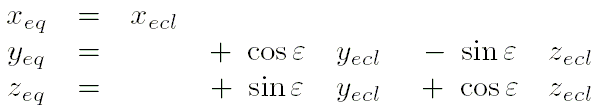 , ,
|
(35)
|
где угол наклонения эклиптики к экватору на эпоху J2000 равен
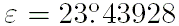 .
.
10.2. Решение уравнения Кеплера
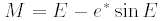 .
.
Зададим числовые значения средней аномалии
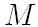 (в градусах)
и эксцентриситета
(в градусах)
и эксцентриситета 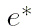 (в градусах),
вычислим начальное значение эксцентрической аномалии
(в градусах),
вычислим начальное значение эксцентрической аномалии
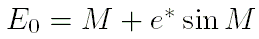 , ,
|
(36)
|
и методом итераций при
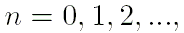 пока
пока
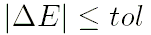 с помощью трёх следующих уравнений
найдём искомое значение эксцентрической аномалии.
Для приближённых вычислений в данном контексте численного значения
с помощью трёх следующих уравнений
найдём искомое значение эксцентрической аномалии.
Для приближённых вычислений в данном контексте численного значения
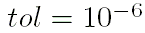 вполне достаточно.
(Отметим,
что величина
вполне достаточно.
(Отметим,
что величина 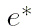 задана в градусах,
а величина
задана в градусах,
а величина 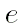 - то же самое значение эксцентриситета в радианах.)
- то же самое значение эксцентриситета в радианах.)
10.3. Значения кеплеровских параметров орбит для вычислений с низкой точностью
В таблице 8.1 даны оценки точностей, которые можно ожидать при использовании приближённого подхода, излагаемого в этом разделе.
Таблица 10.1
Максимальные ошибки в гелиоцентрической долготе λ,
гелиоцентрической широте φ
и гелиоцентрическом расстоянии планеты ρ,
возникающие в результате применения приближённых формул данного раздела.
Интервал с 1800 года по 2050 год.
|
планета
|
λ ["]
|
φ ["]
|
ρ [1000 км]
|
|
Меркурий
|
15
|
1
|
1
|
|
Венера
|
20
|
1
|
4
|
|
Земля+Луна
|
20
|
8
|
6
|
|
Марс
|
40
|
2
|
25
|
|
Юпитер
|
400
|
10
|
600
|
|
Сатурн
|
600
|
25
|
1500
|
|
Уран
|
50
|
2
|
1000
|
|
Нептун
|
10
|
1
|
200
|
|
Плутон
|
5
|
2
|
300
|
Интервал с -3000 года по 3000 год.
|
планета
|
λ ["]
|
φ ["]
|
ρ [1000 км]
|
|
Меркурий
|
20
|
15
|
1
|
|
Венера
|
40
|
30
|
8
|
|
Земля+Луна
|
40
|
15
|
15
|
|
Марс
|
100
|
40
|
30
|
|
Юпитер
|
600
|
100
|
1000
|
|
Сатурн
|
1000
|
100
|
4000
|
|
Уран
|
2000
|
30
|
8000
|
|
Нептун
|
400
|
15
|
4000
|
|
Плутон
|
400
|
100
|
2500
|
Таблица 10.2
Кеплеровские элементы и скорости их изменения в системе средних эклиптики и экватора на эпоху J2000, пригодные на интервале времени с 1800 года по 2050 год.
Цифрами в колонках таблицы обозначены:
|
1
|
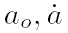
|
а.е, а.е. за столетие
|
|
2
|
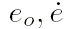
|
радиан, радиан за столетие
|
|
3
|
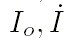
|
градусы, градусы за столетие
|
|
4
|
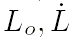
|
градусы, градусы за столетие
|
|
5
|
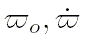
|
градусы, градусы за столетие
|
|
6
|
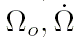
|
градусы, градусы за столетие
|
_______________________________________________________________________________________
1 2 3 4 5 6
Меркурий 0.38709927 0.20563593 7.00497902 252.25032350 77.45779628 48.33076593
0.00000037 0.00001906 -0.00594749 149472.67411175 0.16047689 -0.12534081
Венера 0.72333566 0.00677672 3.39467605 181.97909950 131.60246718 76.67984255
0.00000390 -0.00004107 -0.00078890 58517.81538729 0.00268329 -0.27769418
Земля+Луна 1.00000261 0.01671123 -0.00001531 100.46457166 102.93768193 0.0
0.00000562 -0.00004392 -0.01294668 35999.37244981 0.32327364 0.0
Марс 1.52371034 0.09339410 1.84969142 -4.55343205 -23.94362959 49.55953891
0.00001847 0.00007882 -0.00813131 19140.30268499 0.44441088 -0.29257343
Юпитер 5.20288700 0.04838624 1.30439695 34.39644051 14.72847983 100.47390909
-0.00011607 -0.00013253 -0.00183714 3034.74612775 0.21252668 0.20469106
Сатурн 9.53667594 0.05386179 2.48599187 49.95424423 92.59887831 113.66242448
-0.00125060 -0.00050991 0.00193609 1222.49362201 -0.41897216 -0.28867794
Уран 19.18916464 0.04725744 0.77263783 313.23810451 170.95427630 74.01692503
-0.00196176 -0.00004397 -0.00242939 428.48202785 0.40805281 0.04240589
Нептун 30.06992276 0.00859048 1.77004347 -55.12002969 44.96476227 131.78422574
0.00026291 0.00005105 0.00035372 218.45945325 -0.32241464 -0.00508664
Плутон 39.48211675 0.24882730 17.14001206 238.92903833 224.06891629 110.30393684
-0.00031596 0.00005170 0.00004818 145.20780515 -0.04062942 -0.01183482
_______________________________________________________________________________________
Таблица 10.3
Кеплеровские элементы и скорости их изменения в системе средних эклиптики и экватора на эпоху J2000, пригодные на интервале времени с -3000 года по 3000 год. Вычисление значений средней аномалии 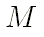 внешних планет от Юпитера до Плутона необходимо выполнять по формуле (30), то есть с дополнительными слагаемыми. Числовые значения добавочных коэффициентов даны в таблице 10.4.
внешних планет от Юпитера до Плутона необходимо выполнять по формуле (30), то есть с дополнительными слагаемыми. Числовые значения добавочных коэффициентов даны в таблице 10.4.
_______________________________________________________________________________________
1 2 3 4 5 6
Меркурий 0.38709843 0.20563661 7.00559432 252.25166724 77.45771895 48.33961819
0.00000000 0.00002123 -0.00590158 149472.67486623 0.15940013 -0.12214182
Венера 0.72332102 0.00676399 3.39777545 181.97970850 131.76755713 76.67261496
-0.00000026 -0.00005107 0.00043494 58517.81560260 0.05679648 -0.27274174
Земля+Луна 1.00000018 0.01673163 -0.00054346 100.46691572 102.93005885 -5.11260389
-0.00000003 -0.00003661 -0.01337178 35999.37306329 0.31795260 -0.24123856
Марс 1.52371243 0.09336511 1.85181869 -4.56813164 -23.91744784 49.71320984
0.00000097 0.00009149 -0.00724757 19140.29934243 0.45223625 -0.26852431
Юпитер 5.20248019 0.04853590 1.29861416 34.33479152 14.27495244 100.29282654
-0.00002864 0.00018026 -0.00322699 3034.90371757 0.18199196 0.13024619
Сатурн 9.54149883 0.05550825 2.49424102 50.07571329 92.86136063 113.63998702
-0.00003065 -0.00032044 0.00451969 1222.11494724 0.54179478 -0.25015002
Уран 19.18797948 0.04685740 0.77298127 314.20276625 172.43404441 73.96250215
-0.00020455 -0.00001550 -0.00180155 428.49512595 0.09266985 0.05739699
Нептун 30.06952752 0.00895439 1.77005520 304.22289287 46.68158724 131.78635853
0.00006447 0.00000818 0.00022400 218.46515314 0.01009938 -0.00606302
Плутон 39.48686035 0.24885238 17.14104260 238.96535011 224.09702598 110.30167986
0.00449751 0.00006016 0.00000501 145.18042903 -0.00968827 -0.00809981
_______________________________________________________________________________________
Таблица 10.4
Дополнительные слагаемые, которые должны быть добавлены при вычислении средней аномалии внешних планет от Юпитера до Плутона на интервале времени от -3000 года до 3000 года (формула 30).
_______________________________________________________________
b c s f
Юпитер -0.00012452 0.06064060 -0.35635438 38.35125000
Сатурн 0.00025899 -0.13434469 0.87320147 38.35125000
Уран 0.00058331 -0.97731848 0.17689245 7.67025000
Нептун -0.00041348 0.68346318 -0.10162547 7.67025000
Плутон -0.01262724
_______________________________________________________________
Единицы измерения коэффициентов следующие:
b - градусы в столетие за столетие,
c - градусы,
s - градусы,
f - градусы за столетие.
Вернуться на страничку "забвения".
Все графические изображения математических формул и знаков
скопированы из оригинальной версии
статьи.
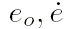
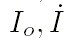
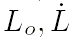
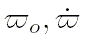
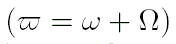 ,
,
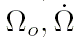
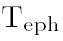 , надо выполнить следующие действия:
, надо выполнить следующие действия:
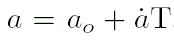 ,
,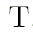 - момент времени в юлианских столетиях от эпохи J2000:
- момент времени в юлианских столетиях от эпохи J2000: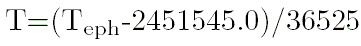 .
.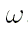 и значение средней аномалии
и значение средней аномалии 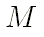 :
: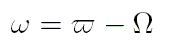 ,
,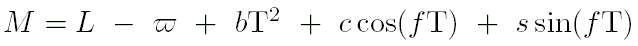 ,
,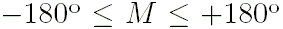
 путём решения уравнения Кеплера:
путём решения уравнения Кеплера: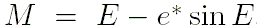 ,
,
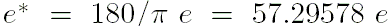 .
.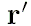 , расположенный в её орбитальной плоскости, с осью
, расположенный в её орбитальной плоскости, с осью 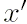 , направленной из фокуса эллипса в точку перигелия:
, направленной из фокуса эллипса в точку перигелия: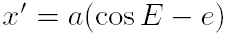 ,
,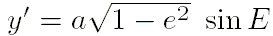 ,
,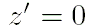 .
.
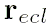 , лежащий в плоскости эклиптики, фиксированной на стандартную эпоху J2000, с осью абсцисс, направленной в точку равноденствия:
, лежащий в плоскости эклиптики, фиксированной на стандартную эпоху J2000, с осью абсцисс, направленной в точку равноденствия: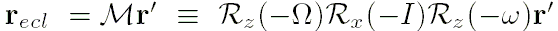 ,
,
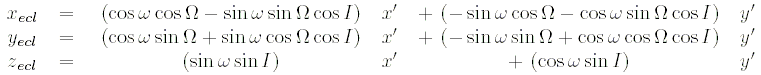 ,
,
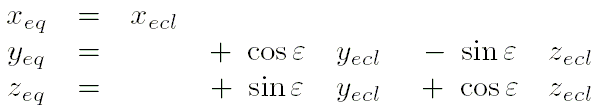 ,
,
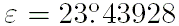 .
. 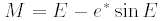 .
.
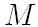 (в градусах)
и эксцентриситета
(в градусах)
и эксцентриситета 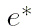 (в градусах),
вычислим начальное значение эксцентрической аномалии
(в градусах),
вычислим начальное значение эксцентрической аномалии
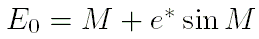 ,
,
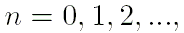
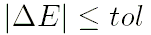
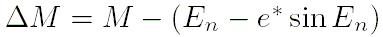 ,
,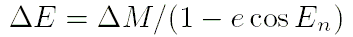 ,
,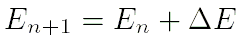 ,
,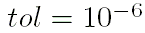 вполне достаточно.
(Отметим,
что величина
вполне достаточно.
(Отметим,
что величина 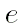 - то же самое значение эксцентриситета в радианах.)
- то же самое значение эксцентриситета в радианах.)