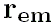 и
и
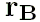 , даваемые формулами
, даваемые формулами
Orbital Ephemerides of the Sun, Moon, and Planets
presented by E. Myles Standish and James G. Williams
| до того | Содержание | после того |
Орбитальные эфемериды Солнца, Луны и планет.
Е.Майлс Стэндиш, Джеймс Г.Вильямс
4. Алгоритм численного интегрирования
Численное интегрирование уравнений (1), (6), (8) выполняется методом Адамса с переменной длиной шага и переменным порядком интегрирования (Krogh, 1972). Текущий порядок интегрирования 33 дифференциальных уравнений определяется заданием границы погрешностей и поведением обратных разностей для ускорений.
Это доказано численно, что более удобно интегрировать уравнения движения Луны
относительно Земли, чем относительно барицентра Солнечной системы. Барицентрические
положения Земли и Луны
были заменены на величины
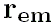 и
и
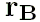 , даваемые формулами
, даваемые формулами
и
где обозначения
e
и
m
относятся к Земле и Луне, соответственно.
Заметим, что
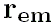 является разницей векторов
в барицентрической системе отсчёта и отличается
от геоцентрического вектора релятивистским преобразованием
между барицентрической и геоцентрической
небесными опорными системами отсчёта.
(Вектор
является разницей векторов
в барицентрической системе отсчёта и отличается
от геоцентрического вектора релятивистским преобразованием
между барицентрической и геоцентрической
небесными опорными системами отсчёта.
(Вектор
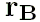 можно интерпретировать как положение
ньютоновского центра масс системы Земля-Луна
относительно барицентра Солнечной системы.
Он не имеет физического смысла и не должен появляться при вычислениях сил;
это исключительно средство
для улучшения численного поведения дифференциальных уравнений.)
можно интерпретировать как положение
ньютоновского центра масс системы Земля-Луна
относительно барицентра Солнечной системы.
Он не имеет физического смысла и не должен появляться при вычислениях сил;
это исключительно средство
для улучшения численного поведения дифференциальных уравнений.)
4.1. Оценка ошибки интегрирования
Метод контроля ошибки, использованный при интегрировании,
ставит предел абсолютного значения оцениваемой погрешности в скорости
для каждого уравнения на конце каждого шага интегрирования.
Величина шага и порядок интегрирования улучшались на основе оцениваемой погрешности.
Предел, выбранный для модели DE405/LE405, был
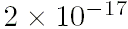 астрономических единиц за сутки для каждого компонента уравнений движения
планет и Луны и
астрономических единиц за сутки для каждого компонента уравнений движения
планет и Луны и
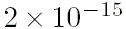 радиан за сутки для каждого компонента уравнений либрации.
радиан за сутки для каждого компонента уравнений либрации.
Интегрирование уравнений движения в случае моделей, предшествующих DE405, было выполнено на компьютере Univac mainframe с двойной точностью и 60-битовой мантиссой. Решение для DE405 было получено с четверной точностью на компьютере VAX Alpha. Во всех случаях ошибка интегрирования была значительно меньше, чем оценка погрешности, получаемая из невязок процесса улучшения начальных условий и постоянных модели с помощью наблюдательных данных. Эти погрешности проанализированы позже в разделе 9.
4.2. Улучшенные постоянные
Интегрирование требует ввода числовых значений ряда параметров. Часть этих параметров, таких как начальные положения и скорости планет и Луны, являются результатом процедуры улучшения по методу наименьших квадратов и отличаются на каждой итерации. Другие параметры, такие как массы планет и числовые значения коэффициентов разложения геопотенциала, взяты из внешних источников и были лишь чуть-чуть изменены для целей построения модели. Несколько параметров, такие как масса системы Земля-Луна, могут быть улучшены на основе наблюдений, но для удобства подправлялись только тогда, когда статистически значимые улучшенные значения параметра выходили за пределы стандартного интервала.
Список начальных значений и динамических постоянных, использованных при интегрировании уравнений движения в процессе создания модели DE405/LE405, дан в разделе 8. В том же разделе есть список постоянных, использованных для редукции наблюдательных данных, которые были определены при решении по методу наименьших квадратов.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |