Планета-гигант обращается вокруг Солнца по круговой орбите. У планеты-гиганта есть спутник. Записаны канонические уравнения движения спутника в невращающейся системе отсчёта.

В аннотации к статье

А.А.Орлов
Приближённое аналитическое представление пространственных движений в задаче Хилла
"Бюллетень Института теоретической астрономии АН СССР"
(1965, том X, №5, с.360-378)

сказаны следующие слова:

Применяется метод Делоне-Цейпеля к решению дифференциальных уравнений, лежащих в основе хилловой теории Луны. Получены приближённые формулы, представляющие пространственные движения спутника. Разложения в ряды по степеням эксцентриситета и наклонности не применяются.
Окончательные формулы дают вековые возмущения в элементах орбиты спутника с точностью до величин порядка m³, а периодические возмущения - с точностью до членов порядка m, где m отношение среднего движения возмущающего тела к среднему движению спутника.

В первом разделе статьи дан всё тот же текст аннотации, но немного расширенный.

Целью настоящей работы является построение решения дифференциальных уравнений, лежащих в основе хилловой теории Луны (Hill, 1878), в случае, когда наклон орбиты спутника к плоскости движения возмущающего тела может быть произвольным. При этом используется метод Делоне-Цейпеля (Delaunau, 1860; Zeipel, 1916), успешно приложенный Брауэром (Brouwer, 1959) и другими авторами к исследованию движения спутника осесимметричной планеты.
Приложение метода Делоне-Цейпеля к исследованию плоских движений в задаче Хилла позволяет, как и в случае движения спутника сфероидальной планеты, получить решение задачи, не прибегая к разложению искомых функций по степеням эксцентриситета, в виде тригонометрических рядов (Gen-ishiro Hori, 1963). В случае же пространственных движений решение задачи Хилла оказывается более сложным делом. Как мы увидим ниже, построить даже приближённые формулы, представляющие пространственные движения спутника, не прибегая к разложениям в ряды по степеням эксцентриситета, можно только с помощью эллиптических функций.
В настоящей работе получены формулы, представляющие пространственные движения в задаче Хилла со следующей точностью: вековые члены - с учётом третьей степени отношения среднего движения n₂ возмущающего тела к среднему движению n₁ спутника, а периодические члены - с точностью до величин первого порядка относительно n₂/n₁ включительно.

Текст строгий. Текст математический. Безусловно, понятный в 1965 году главному редактору "Бюллетеня ИТА". Джордж Уильям Хилл записал дифференциальные уравнения специального вида при изучении возмущений от Солнца в движении Луны. В изучаемой нами работе автор решил уравнения задачи Хилла с помощью оригинального метода. Разумеется, А.А.Орлов не имел в виду приложение своих исследований к движению Луны. Он строил модель движения далёких спутников планет-гигантов, но написал об этом одну строчку в самом конце статьи. Если решение, представленное Джорджом У. Хиллом, применимо только для плоских движений, то приближённые формулы, полученные А.А.Орловым, справедливы для любых значений эксцентриситета и угла наклонения орбиты спутника планеты, обращающейся вокруг Солнца (или какой-либо другой звезды) по круговой орбите.

Второй раздел начинается с подробной постановки задачи.

Предположим, что точка P₁ массы m₁ движется вблизи точки P₀ массы m₀, причём её движение возмущается точкой P₂ имеющей массу m₂ и движущейся по круговой кеплеровой орбите радиуса a₂ вокруг центра масс системы (m₀, m₁). Введём систему координат P₀x₁y₁z₁ с началом в точке P₀ и осью P₀z₁, перпендикулярной плоскости круговой орбиты точки P₂. Наряду с этим рассмотрим систему координат Cx₂y₂z₂ с началом в центре масс системы (m₀, m₁) и осями, параллельными соответствующим осям системы P₀x₁y₁z₁. Движение точки P₁ мы будем относить к системе P₀x₁y₁z₁, а движение точки P₂ - к системе Cx₂y₂z₂. В таком случае координаты точек P₁ и P₂ выразятся следующими формулами

где r и v - радиус-вектор и истинная аномалия спутника P₁, движущегося по орбите, определяемой следующими оскулирующими элементами: большой полуосью a, эксцентриситетом e, наклонностью i, средней аномалией M, долготой восходящего узла Ω, отсчитываемой от положительного направления оси P₀x, и угловым расстоянием перицентра от восходящего узла ω. В формулах (1.2) l₂ - долгота возмущающей точки P₂, отсчитываемой от положительного направления оси Cx₂.
Будем предполагать, что 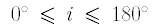, причём движение точки P₁ является прямым, если 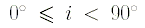, и обратным, если .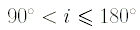

Как известно из курса небесной механики, силовая функция описанной выше задачи имеет вид

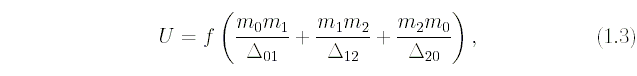
где 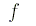- постоянная тяготения, 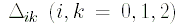есть расстояние между точками P_i и P_k.

Положим

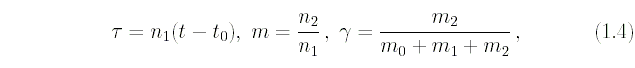
где

- постоянное среднее движение спутника P₁;
a₁ - большая полуось кеплеровой эллиптической орбиты, соответствующая этому среднему движению;

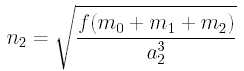
- среднее движение возмущающей точки.
Разлагая функцию U в ряд по степеням отношения r/a₂ и отбрасывая члены, зависящие от произведения m² на первую и более высокие степени r/a₂, мы придём к дифференциальным уравнениям, лежащим в основе хилловой теории Луны, записанной по отношению к невращающейся системе координат:

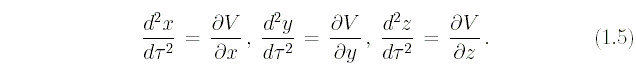
В этих уравнениях

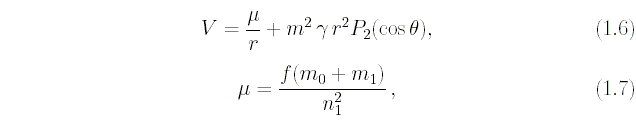
где 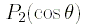- полином Лежандра второго порядка,

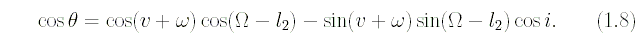
Множитель γ, фигурирующий в формуле(1.6), будет, как показывает третье равенство (1.4), очень близким к единице, если масса возмущающего тела весьма велика по сравнению с суммой m₀+m₁. Поэтому во многих задачах астрономии, в которых возмущающим телом является Солнце, этот множитель можно опустить. Однако, если масса возмущающего тела не будет очень большой по сравнению с m₀+m₁, то заменять γ единицей нельзя.

Далее автор выполняет переход к классическим каноническим элементам Делоне:

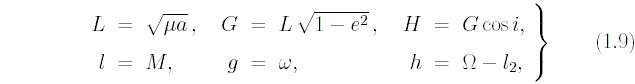
причём в последнем из этих равенств к обычному аргументу h=Ω добавлен член -l₂ для того, чтобы избежать явной зависимости функции Гамильтона от времени.
Элементы L, G, H, l, g, h удовлетворяют следующей системе дифференциальных уравнений:

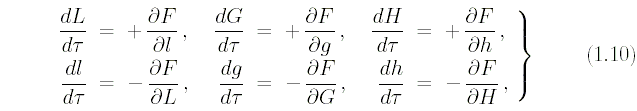
где

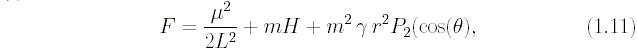
причём 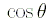можно записать в следующем виде

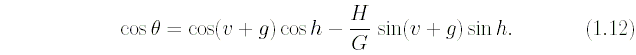
Функции r и v в правой части равенства (1.11) должны быть выражены через элементы (1.9).
Наша задача заключается в получении приближённого решения дифференциальных уравнений (1.10) с точностью, указанной выше
(вековые члены - с учётом третьей степени отношения среднего движения n₂ возмущающего тела к среднему движению n₁ спутника, а периодические члены - с точностью до величин первого порядка относительно n₂/n₁ включительно),
не прибегая к разложениям в ряды по степеням эксцентриситета e, при любом начальном наклоне орбиты спутника к плоскости круговой орбиты возмущающего тела в предположении, что m=n₂/n₁ мало.

Вернуться на страничку
Движение далёких спутников