Полиномы Лежандра и их производные
Рекуррентное соотношение для вычисления полиномов Лежандра высших порядков запишем в виде:
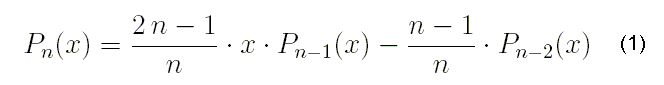
с начальными условиями
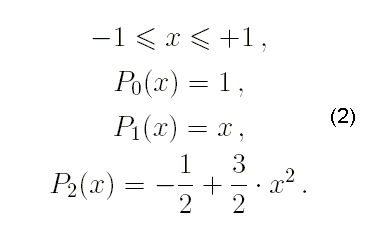
Возможны два варианта применения рекуррентной формулы.
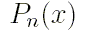 для
произвольного
для
произвольного 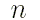 при заданном числовом значении
аргумента
при заданном числовом значении
аргумента 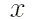 .
.
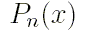 при различных степенях
аргумента
при различных степенях
аргумента 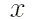 .
.
Преимущество рекуррентных соотношений заключается в скорости достижения результата, недостатком является возможная потеря вычислительной точности при вычитании больших чисел.
Первый вариант может быть проверен с помощью тождеств
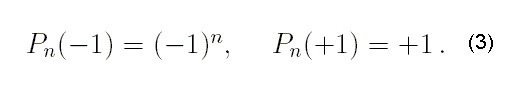
Расчёты показали, что
в результате использования формулы (1)
с начальными условиями (2)
и аргументами 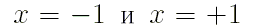 тождества (3)
справедливы с точностью до 15 знаков после запятой
при всех порядках полинома Лежандра от
тождества (3)
справедливы с точностью до 15 знаков после запятой
при всех порядках полинома Лежандра от 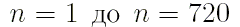 .
.
Второй способ проверки состоит в использовании формулы для производящей функции полиномов Лежандра:
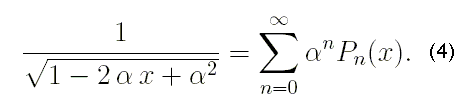
Расчёты показали (табл.1),
что при различных численных
значениях параметра 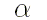 и аргумента
и аргумента 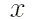 значение суммы в правой части выражения (4)
соответствует значению функции в левой части
с точностью до 12 значащих цифр.
значение суммы в правой части выражения (4)
соответствует значению функции в левой части
с точностью до 12 значащих цифр.
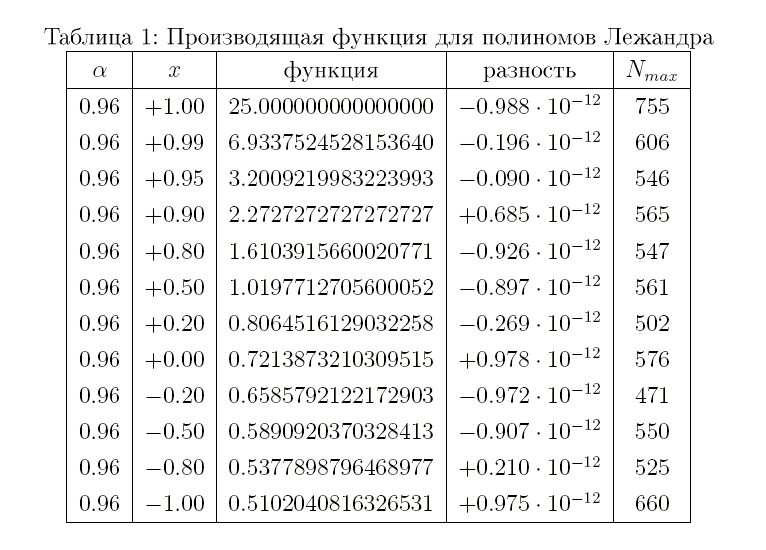
Целое число 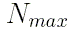 в последней колонке означает наибольший
порядок полинома
в последней колонке означает наибольший
порядок полинома 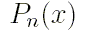 в сумме (4).
Значение
в сумме (4).
Значение 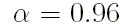 характерно для объектов
с высотой полёта 300 километров над поверхностью Земли.
характерно для объектов
с высотой полёта 300 километров над поверхностью Земли.
Для параметра 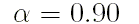 , присущего
геодезическим спутникам с высотой полёта более 700 километров,
значение
, присущего
геодезическим спутникам с высотой полёта более 700 километров,
значение 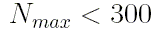 .
.
Вывод:
для заданных значений
аргумента 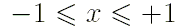 численные значения полиномов
численные значения полиномов 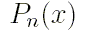 с помощью рекуррентного алгоритма
определяются практически без потери вычислительной точности.
с помощью рекуррентного алгоритма
определяются практически без потери вычислительной точности.
Второй вариант используется на предварительной стадии преобразования возмущающей функции.
Пусть 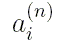 -
численные коэффициенты полинома
-
численные коэффициенты полинома
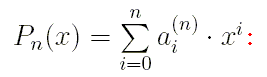
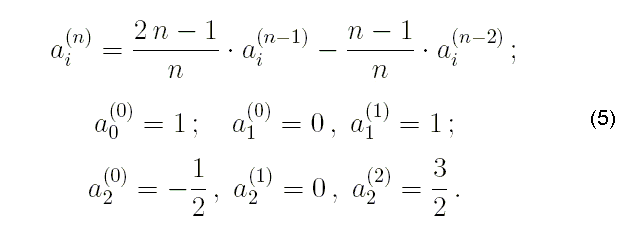
Сумма коэффициентов полинома любого порядка всегда равна единице
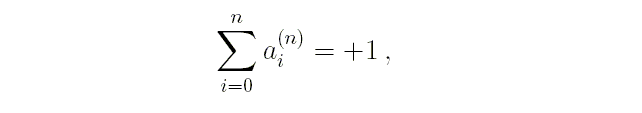
но величины коэффициентов достигают больших значений.
В табл.2 приводятся числовые значения некоторых коэффициентов:

Большое количество нулей после восемнадцатой значащей цифры каждого числа возникает как следствие ограниченности разрядной сетки компьютера.
Вывод:
алгоритм (5)
определения значений коэффициентов
полинома 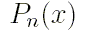 при различных степенях аргумента
при различных степенях аргумента 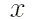 приводит к потере вычислительной точности в случае
полиномов высоких порядков.
Для
приводит к потере вычислительной точности в случае
полиномов высоких порядков.
Для 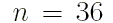 погрешность может оказаться в пятом знаке после запятой.
При значениях
погрешность может оказаться в пятом знаке после запятой.
При значениях 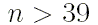 нет смысла
использовать полученные коэффициенты.
нет смысла
использовать полученные коэффициенты.
Рекуррентное соотношение для вычисления производных высших порядков от полиномов Лежандра запишем в виде:
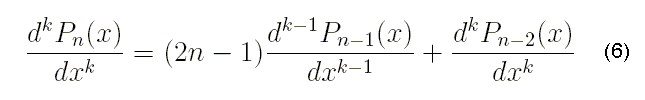
с начальными условиями для всех значений 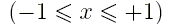
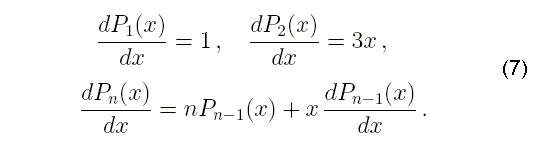
Каждая из производных
представляет из себя полином
относительно аргумента
Точность вычисления производных
при заданном числовом значении аргумента
Расчёты показали,
что
в результате использования формулы (6)
с различными значениями
аргумента
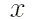 порядка
порядка 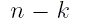 .
.
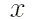 можно проверить с помощью соотношений:
можно проверить с помощью соотношений:
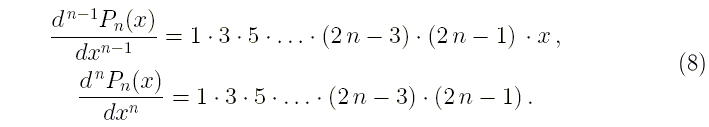
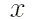 тождества (8)
справедливы с точностью до 17 значащих цифр
при всех порядках полинома Лежандра от
тождества (8)
справедливы с точностью до 17 значащих цифр
при всех порядках полинома Лежандра от
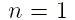 до
до
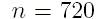 .
.
Вывод:
рекуррентные формулы (6), (7)
можно применять
для вычисления мгновенных значений
правых частей
в алгоритме численного
интегрирования уравнений движения.
В аналитическом подходе
надо знать числовые значения
коэффициентов 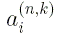 полиномов
полиномов
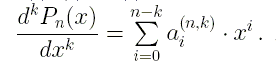
Алгоритм имеет вид:
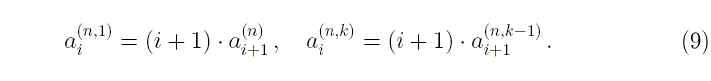
Сравним по порядку величины две пары коэффициентов:
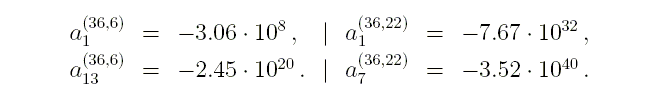
Вывод:
в процессе вычисления производных 6-го порядка от
Здесь можно вернуться на страницу Тексты и алгоритмы